Расчет ветровой нагрузки по СП 20.13330.2016
Аннотация. В статье описано, как определить ветровую нагрузку с помощью руководящего документа. В СП 20.13330.2016 для учета ветровой нагрузки предписывается сделать расчет на «основную ветровую нагрузку», «пиковую ветровую нагрузку», а также сделать проверку на возникновение вихревого возбуждения, галопирование, дивергенции и флаттера. При этом, как и положено руководящему документу, приведенные термины приводятся без объяснений физической сути. Как результат, неискушенный проектировщик может сразу не понять, чем «пиковая ветровая нагрузка» отличается от «пульсационной ветровой нагрузки» и какой именно аэродинамический коэффициент ему нужен. По этой причине в начале статьи приведено описание основных свойств ветрового потока и физическая модель воздействия ветра на сооружение. Эти знания необходимы для понимания терминов СП «Нагрузки и воздействия» и их правильного применения для расчета ветровых нагрузок.
Оглавление статьи
- Свойства ветрового потока
- Физическая модель воздействия ветра на здание
- Ветровая нагрузка согласно СП 20.13330.2016
3.1 Расчет основной ветровой нагрузки
3.2 Расчет пиковой ветровой нагрузки
3.3 Аэродинамические коэффициенты, используемые в СП
3.4 Границы применимости подходов СП
1. Свойства ветрового потока
Для правильного учета ветровой нагрузки на сооружение необходимо понимать основные особенности ветрового потока. Ветровой поток – это движение воздуха над земной поверхностью из области повышенного к области с пониженным давлением. Во время движения ветер взаимодействует с расположенной на земной поверхности шероховатостью: горы, холмы, леса, поля, моря, градостроительные объекты, что приводит к сильному изменению характеристик ветрового потока в зависимости от высоты над поверхностью земли. В связи с этим, на каждой высотной отметке можно наблюдать развитое турбулентное движение, которое характеризуется беспорядочным изменением скорости потока во времени. Пример зависимости изменения скорости от времени приведен на рисунке-1.
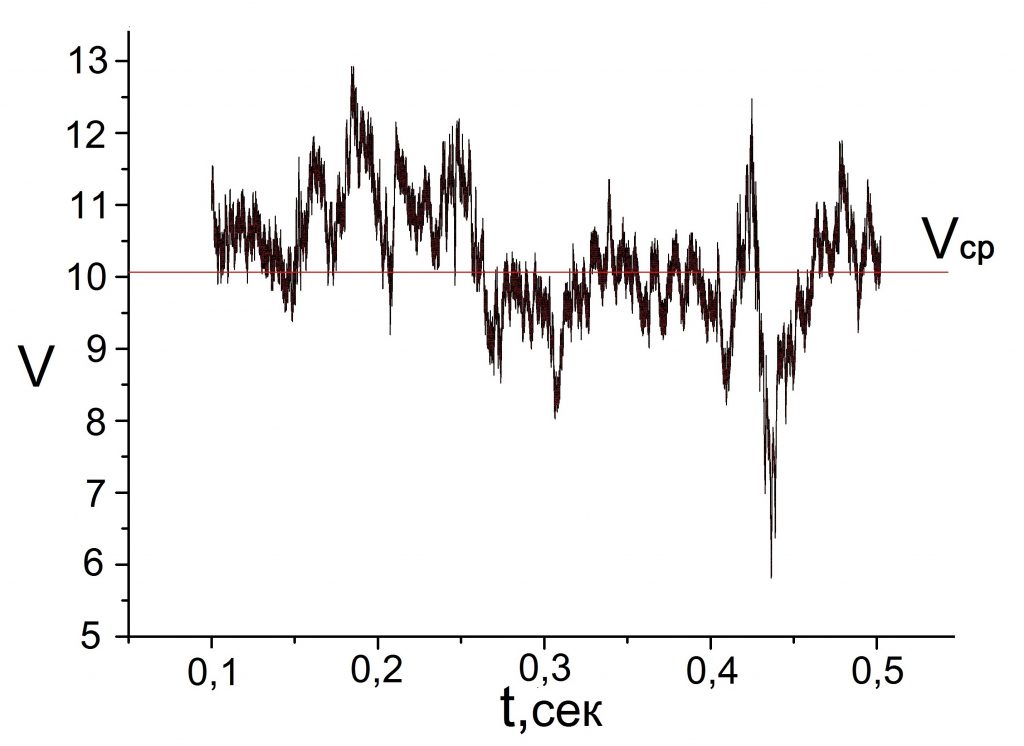
Рисунок 1 – Изменение значений скорости воздушного потока во времени
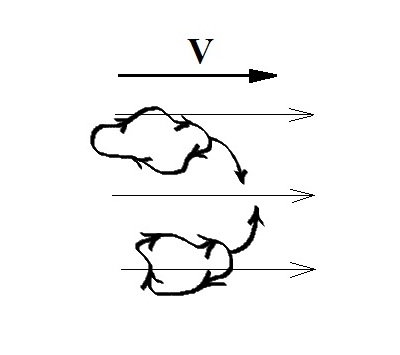
Для описания турбулентного движения используют математический аппарат теории вероятности и описание турбулентного потока, как сумму средней и пульсационной составляющей скорости. Для физического описания турбулентности также используется понятие деформируемые вязкие объемы – это маленькие частички потока, которые имеют определенный физический размер (масштаб турбулентности). С некоторым допущением их можно назвать турбулентными вихрями. Они движутся вместе с основным потоком, но при этом их форма все время деформируются, а сами они хаотично перемещаются на небольшие расстояния в любом направлении по отношению к основному потоку, как показано на рисунке 2.
Рассмотрим основные понятия, используют в аэродинамике для описания потока которые важно знать для понимания терминов, которые приведены в СП «Нагрузки и воздействия».
Средняя скорость потока – осредненное во времени значение скорости потока. Для ее оценки важно правильно выбрать временной интервал осреднения. Он с одной стороны должен быть значительно больше периода нестационарных турбулентных пульсаций, с другой стороны – меньше времени, за которое происходит качественное изменение характера течения. В задачах строительной аэродинамики в большинстве стран, в том числе в России, принято десятиминутное осреднение.
Пульсация скорости потока – пульсационная составляющая скорости потока, вызванная его турбулентностью (турбулентными вихрями). Она описывается такой характеристикой как интенсивность турбулентности.
Масштаб турбулентности физический смысл которого состоит в характерном размере турбулентных вихрей. В турбулентном потоке одновременно присутствуют вихри разных физических размеров.
Частотный спектр пульсаций скорости, который показывает распределение энергии потока по различным частотам (масштабам вихрей). Существует множество различных зависимостей, аппроксимирующих частотные спектры. Один из самых распространенных для описания пульсаций ветра в пограничном слое атмосферы – спектр Кармана изображенный на рисунке 5. Легко увидеть, что максимальной энергией в турбулентном приземном потоке обладают порывы (турбулентные вихри) с частотой пульсации равно 0.02 Гц.
Коэффициент пространственной корреляции пульсаций давления – статистическая взаимосвязь значений давления в двух точках (областях).
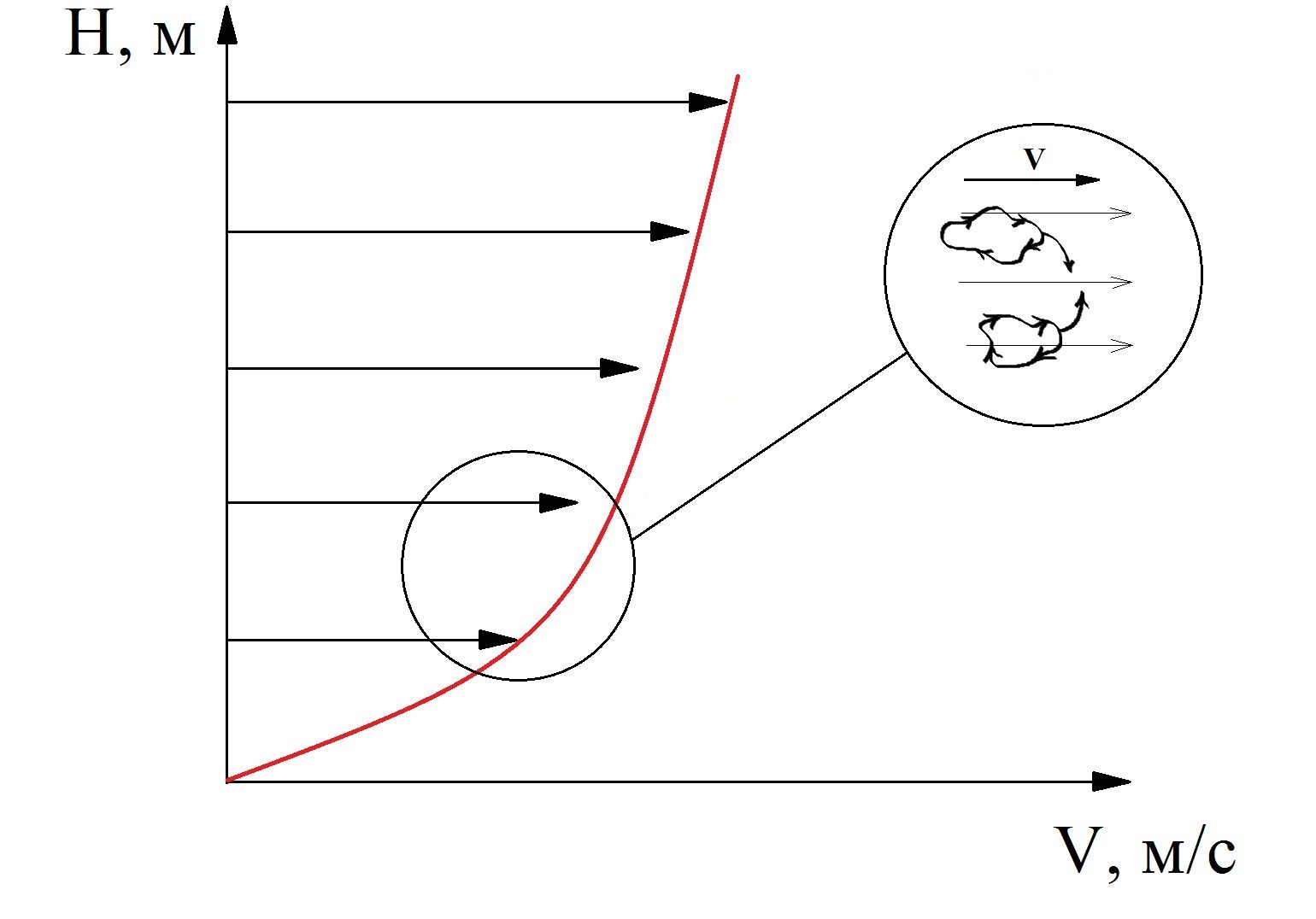
Рисунок 3 — Зависимость изменения средней составляющей скорости ветра от высоты
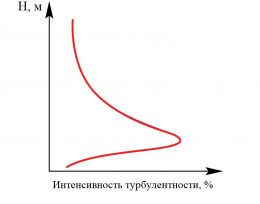
Рисунок 4 — Зависимость изменения пульсационной оставляющей скорости ветра от высоты
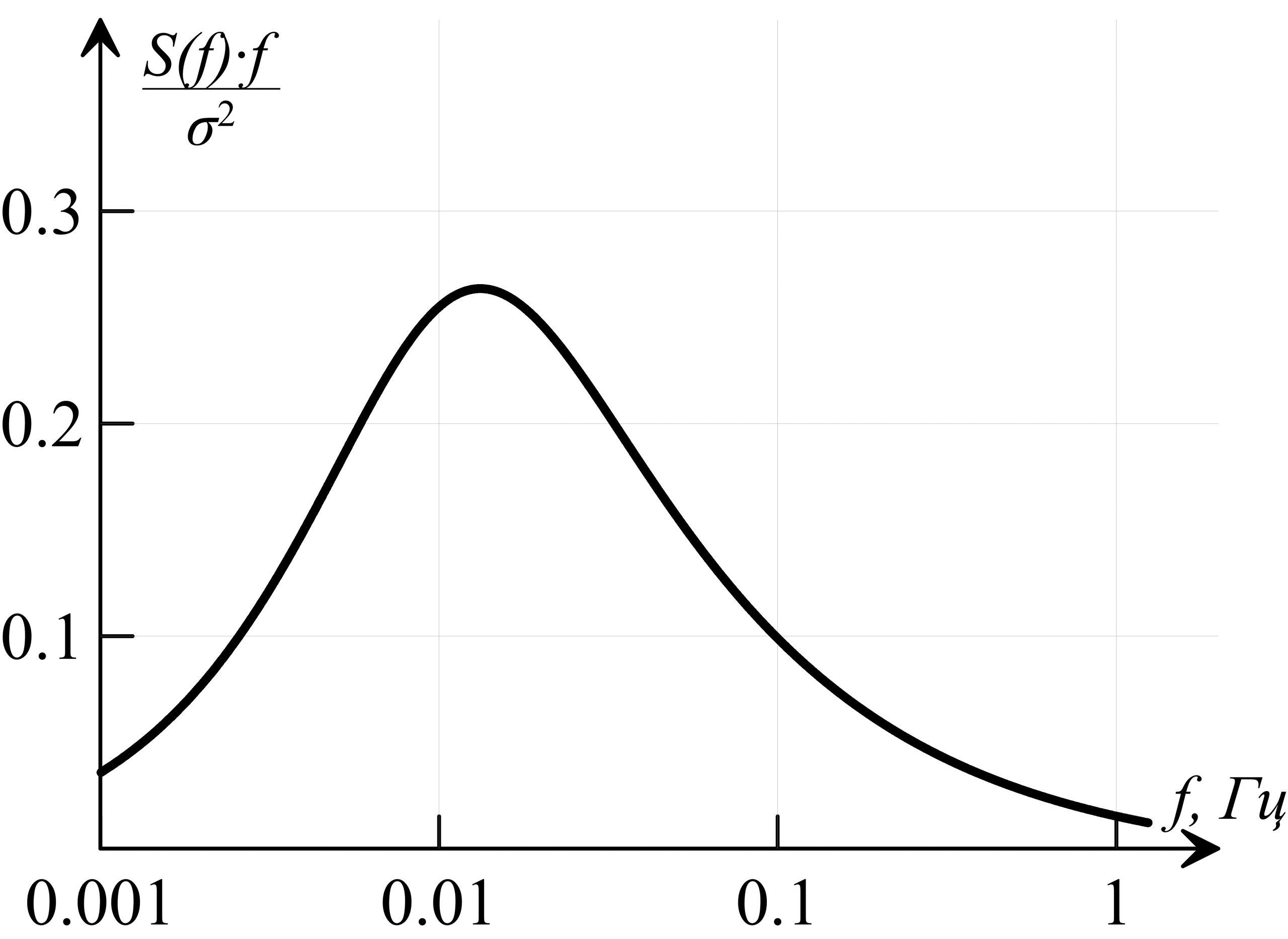
Рисунок 5 — Частотный спектр пульсаций скорости ветра
2. Физическая модель воздействие ветра на здание
При воздействии пограничного слоя атмосферы на сооружение на различных его поверхностях возникает локальная нестационарная нагрузка в виде ветрового давления, которая существенно меняется (пульсирует) во времени. Если рассматривать локальную поверхность здания (либо конкретную точку) и действие на нее турбулентного ветра, то будет видна картина, подобная той, что приведена на рисунке 6. На этой локальной поверхности будет реализовываться изменяющееся во времени ветровое давление. Если посмотреть на максимумы ветрового давления на этой зависимости, то можно увидеть, что они приходятся на максимумы пульсаций скорости ветрового потока. Согласно СП «Нагрузки и воздействия» это называется термином «пиковая ветровая нагрузка». Иными словами «пиковая ветровая нагрузка» – это статистический максимум нагрузки от турбулентного ветра на локальную поверхность (точку) фасада здания. При этом важно не забывать, что пиковая ветровая нагрузка зависит не только от ветра, а также от формы здания и других факторов.
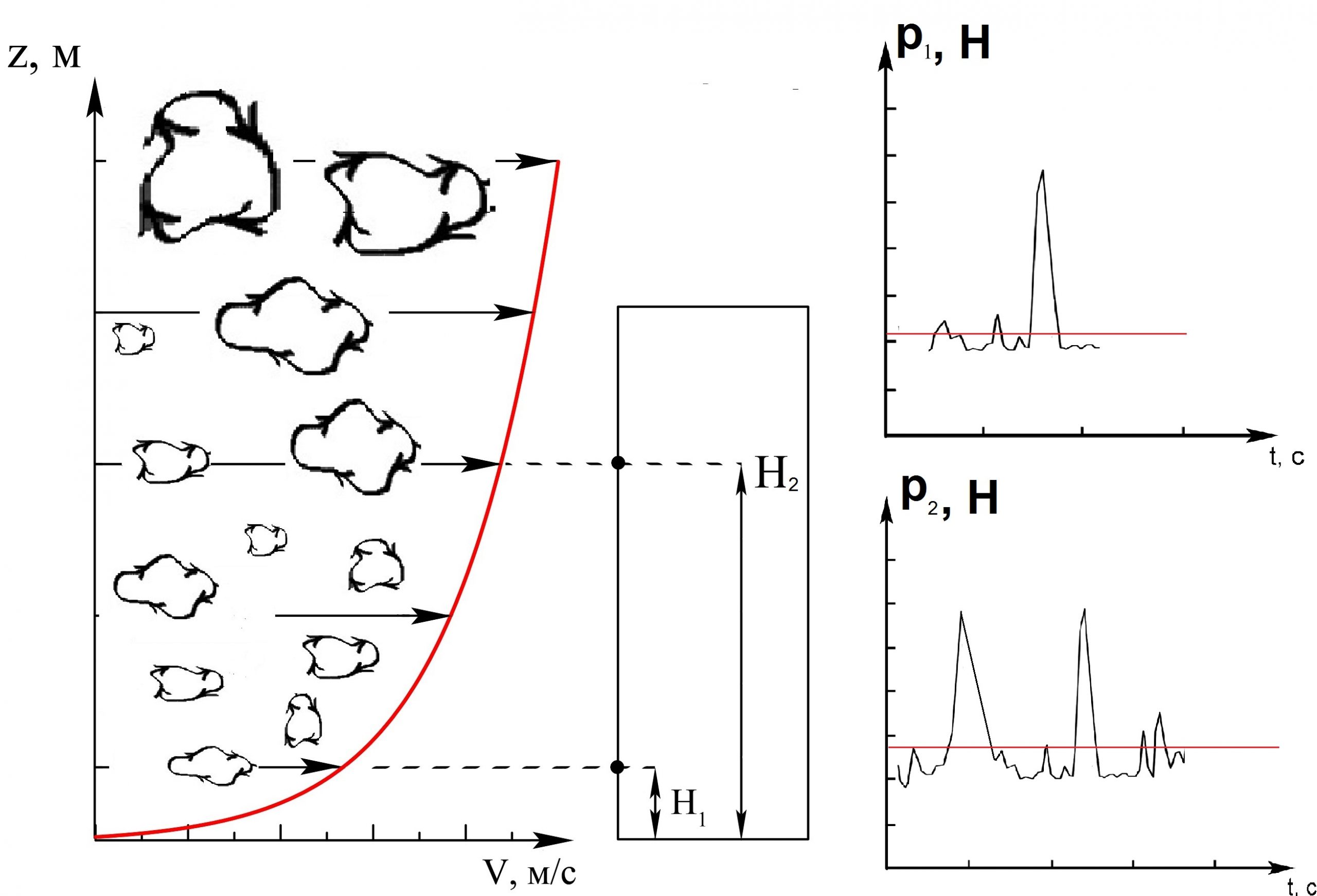
Рисунок 6 – Воздействие пограничного слоя атмосферы на здание
Если для каждого момента времени правильно проинтегрировать ветровую нагрузку по соседним локальным поверхностям всего здания, то получим значение ветровой нагрузки в целом на сооружение для конкретного мгновения времени. Таким образом, получим зависимость ветровой нагрузки на элемент сооружения от времени наблюдения. Это и будет ветровая нагрузка, которая называется в СП «Нагрузки и воздействия» термином «основная ветровая нагрузка» В этом случае автоматически будут учтены корреляция пульсаций ветра и соответственно неодновременность действия пиковой нагрузки на разные элементы фасада.
Следует отметить, что описанная выше картина физического процесса взаимодействия ветрового потока и высотного здания является упрощенной моделью, так как здесь рассмотрен случай двумерного пограничного слоя атмосферы без учета окружающей застройки и влияния орографии.
Основная ветровая нагрузка – это интегральное значение нагрузки от ветра, который действует на все здание в целом. Она используется для расчета фундамента, а также несущих надземных конструкций. Согласно п. 11.1 СП 20.13330.2016 все проектируемые сооружения должны быть проверены на действие основной ветровой нагрузки.
Пиковая ветровая нагрузка – это статистически обоснованное максимальное значение давления на локальном элементе фасада, которое возникает из-за максимальных порывов ветра. Согласно п. 11.2 СП 20.13330.2016 для расчета элементов фасада, а также их узлов крепления нужно использовать пиковую ветровую нагрузку.
Пульсационная ветровая нагрузка – это часть ветровой нагрузки (без средней составляющей), обусловленная нестационарным воздействием ветра, который действует на все здание в целом. Для гибких зданий пульсационная составляющая ветровой нагрузки может вызвать значительный динамический отклик конструкции и привести к недопустимым колебаниям и ускорениям верхних этажей.
3. Ветровая нагрузка согласно СП 20.13330.2016
При проектировании зданий и сооружений в соответствии с требованиями п. 11 необходимо учитывать следующие воздействия ветра:
- основной тип ветровой нагрузки
- пиковые значения ветровой нагрузки, действующие на конструктивные элементы ограждения и узлы их крепления
- резонансное вихревое возбуждение
- аэродинамически неустойчивые колебания типа галопирования, дивергенции и флаттера.
3.1 Расчет основной ветровой нагрузки. В разделе 11.1 приводится на первый взгляд простой и элегантный подход, который указывает, что нормативное значение основной ветровой нагрузки w следует определять как сумму средней wm и пульсационной wg составляющих:
w=wm+wg (1)
Также приводятся формулы, по которым следует определять wm, wp и w0:
wm=w0∙k(ze)∙c (2)
wg=wm∙ζ(ze)∙v (3)
Таким образом, при подстановке (2) и (3) в выражение (1) для определения основной ветровой нагрузки получается простая алгебраическая формула:
w=w0∙k(ze )∙(1+ζ(ze )∙ν)∙c) (4)
В этих формулах учтены основные особенности турбулентного ветрового потока посредством следующих параметров:
- w0 – нормативное ветровое давление – статистическая величина, полученная с помощью обработки многолетних метеорологических наблюдений за скоростью ветра в различных районах РФ;
- k(ze) – коэффициент, учитывающий изменение средней скорости ветра от высоты, а следовательно изменение среднего ветрового давления;
- ζ(ze) – коэффициент, учитывающий изменение пульсации скорости ветра от высоты, а следовательно изменение пульсационной составляющей давления ветра.
Также учтены основные особенности взаимодействия турбулентного ветрового потока со зданием посредством следующих параметров:
- c – аэродинамический коэффициент;
- ν – коэффициент корреляции, который учитывает неодновременность возникновения пиковой ветровой нагрузки сразу на всех поверхностях здания.
Вся сложность нахождения основной ветровой нагрузки по формуле (4) состоит в правильной подстановке аэродинамического коэффициента c и коэффициента корреляции ν. Оба этих коэффициента существенно зависят от архитектурной формы сооружения, направления ветра и окружающей застройки/ландшафта. Поэтому достаточно достоверное обобщение обширных экспериментальных и натурных данных по измерениям аэродинамических коэффициентов и коэффициента корреляции сделаны только для простых архитектурных форм, они приведены в СП 20.13330.2016 в Приложении В.1 и таблице п. 11.1.8. При этом в руководящем документе прямо указано, что во всех других случаях, таких как иная форма сооружения, учет различных направлений (румбов) ветра, наличие близстоящих зданий и сооружений, влияние орографии, сооружения повышенного уровня ответственности, аэродинамические коэффициенты необходимо получать на основе испытаний в специализированных аэродинамических трубах.
3.2 Расчет пиковой ветровой нагрузки. В разделе 11.2 приведена формула для определения пиковой ветровой нагрузки, которую необходимо знать для проектирования элементов ограждения:
w+(-)=w0∙k(ze)∙[1+ζ(ze)]∙cp+(-)∙v+(-) (5)
По своей сути она близка к формуле 4. Сложность в нахождении пиковой ветровой нагрузки также состоит в определении аэродинамического коэффициента давления cp+(-) и коэффициентов корреляции v+(-), данные по которым приведены только для отдельно стоящих прямоугольных в плане зданий. Для всех иных случаев аэродинамические коэффициенты необходимо определять в результате специальных исследований.
Гибкие сооружения и особенно большепролетные мосты подвержены различным видам аэродинамической неустойчивости: вихревое возбуждение, изгибно-крутильный флаттер, срывной флаттер, галопирование, бафтинг, дивергенция. Эти явления имеют разную физическую природу и в случае возникновения приводят к существенным колебаниям конструкции. На ранних стадиях проектирования для оценки возможности их возникновения можно использовать соотношения, приведенные в статье [ссылка на статью].
3.3 Аэродинамические коэффициенты, используемые в СП 20.13330.2016. Отдельное внимание следует уделить использующимся в СП «Нагрузки и воздействия» аэродинамическим коэффициентам. Коэффициенты Cx, Cy, Cz – их еще называют аэродинамическими коэффициентами лобовой силы сопротивления, боковой и вертикальной силы. Они получаются посредством разложения аэродинамической силы, которая действует на здание в целом на три компоненты по осям x, y и z согласно рисунку 7. В практике проектирования строительных конструкций их неудобно применять, так как это интегральные осредненные во времени величины и для их использования необходимо дополнительно указывать точку приложения вектора аэродинамической силы. Большую ценность для проектирования имеют коэффициенты аэродинамического момента, поскольку их можно использовать для учета интегральной нагрузки от ветра, которая приходится на фундамент сооружения. Данные безразмерные коэффициенты составляющих аэродинамической силы и момента определяются по следующим зависимостям:
Cx=(2∙Fx)/(ρ∙V2∙Sлоб ) (6)
Cy=(2∙Fy)/(ρ∙V2∙Sбок ) (7)
Cmx=(2∙Mx)/(ρ∙V2∙Sлоб∙H) (8)
Cmy=(2∙My)/(ρ∙V2∙Sбок∙H) (9)
где V – скорость ветра,
S_лоб – лобовая площадь сооружения,
S_бок – боковая площадь сооружения.
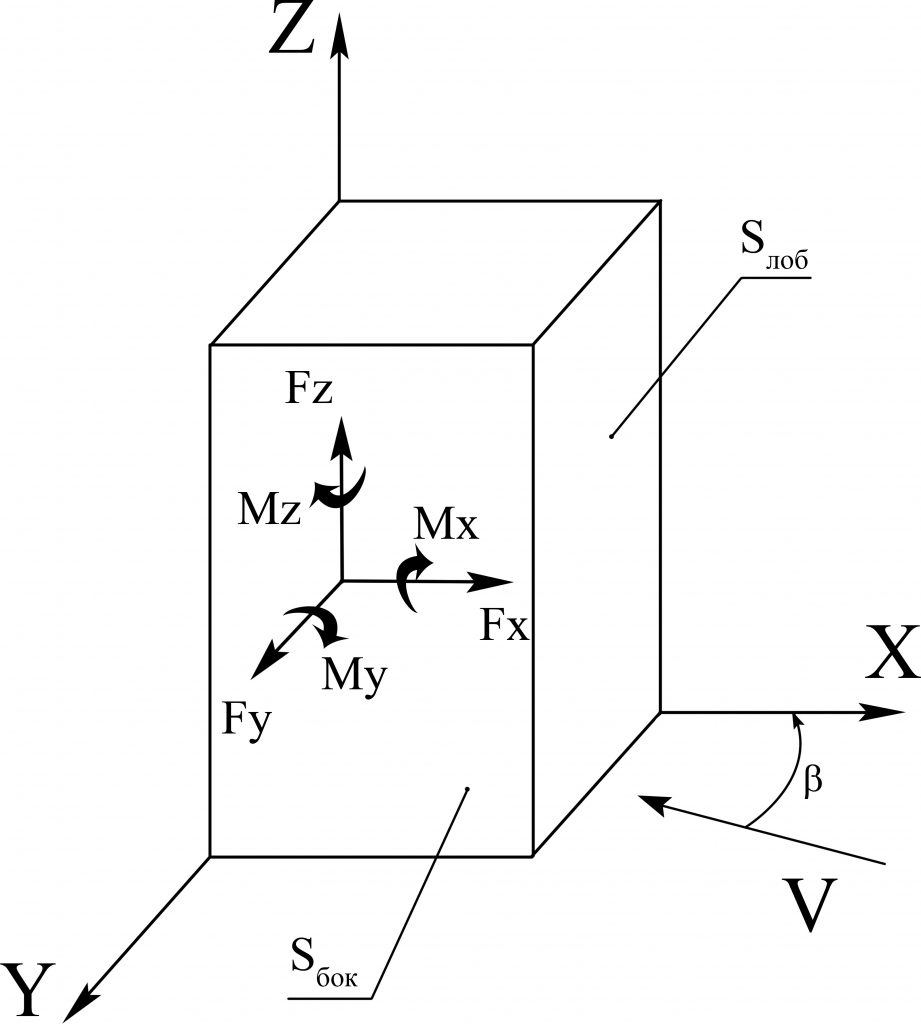
Рисунок 7 – Схема здания в связанной системе координат
Необходимо учитывать, что для нахождения коэффициентов Cx, Cy, Cmx, Cmy используются интегральные осредненные во времени значения компонент аэродинамической силы Fx, Fy, и аэродинамического момента Mx, My. Составляющие Fz и Mz, как правило, имеют малые значения и не учитываются в расчетах ветровой нагрузки на высотные здания.
Аэродинамический коэффициент трения Cf – безразмерная величина силы касательного (тангенциального) трения. Обширные экспериментальные данные по этому коэффициенту имеются только для пластин и удобообтекаемых (без отрывов потока) тел. Например крыловые профили, так как для этих тел вклад сопротивления трения может доходить до 90% от общего сопротивления всего тела. Сложно представить в каком случае в задачах строительной аэродинамики можно обойтись лишь аэродинамическим коэффициентом трения, так как практически все сооружения с точки зрения аэродинамики являются плохообтекаемыми телами. Коэффициент трения можно использовать для дополнительного учета силы трения ветра при сборе нагрузок на фасадные конструкции.
Аэродинамический коэффициент давления – безразмерная величина давления (ветровой нагрузки) в конкретной точке или конечной локальной поверхности сооружения. В литературе по аэродинамике имеет обозначение Cp и определяется по формуле:
Cp=(2∙∆p)/(ρ∙V2 ) (10)
где ∆p – разница между давлением в локальной точке измерения и давлением в свободном воздушном потоке.
В СП 20.13330.2016 используются следующие индексы для обозначения аэродинамического коэффициента давления:
Cpe(или Ce) – коэффициент давления, которое реализуется на внешней поверхности сооружения при его обтекании потоком ветра. Здесь понимается осредненное во времени значение давления;
Cpi (или Ci) – коэффициент давления, которое реализуется на внутренних поверхностях сооружения (с учетом течений внутри сооружения) при его обтекании потоком ветра. Здесь понимается осредненное во времени значение давления. Примером, когда данные о внутреннем давлении необходимо получать и учитывать, могут быть ангары или сухие доки с большими по площади воротами, которые в штатном режиме эксплуатации могут подолгу находиться в открытом состоянии.
Cp+ – пиковое значение аэродинамического коэффициента положительного давления. Это статистический максимум положительной нагрузки от турбулентного ветра на локальную поверхность (точку) фасада с учетом формы здания.
Cp— – пиковое значение аэродинамического коэффициента отрицательного давления. Это статистический максимум отрицательной нагрузки (работающей на отсос, на отрыв) от турбулентного ветра на локальную поверхность (точку) фасада с учетом формы здания.
3.4 Границы применимости подходов СП 20.13330.2016. Как было отмечено ранее, основная сложность нахождения ветровой нагрузки по формуле из руководящего документа состоит в правильной подстановке аэродинамических коэффициентов и коэффициента корреляции ν. Значения этих коэффициентов существенно зависят от архитектурной формы сооружения, направления ветра и окружающей застройки/ландшафта. Поэтому данные по аэродинамическим коэффициентам и коэффициентам корреляции приведены Приложении В.1 и таблице п. 11.1.8 только для простых архитектурных форм.
При этом в руководящем документе прямо указано, что Приложении В.1 не может быть использовано, а аэродинамические коэффициенты необходимо получать на основе специальных исследований в следующих случаях:
- иная форма сооружения,
- учет различных направлений ветра,
- наличие близстоящих зданий и сооружений,
- влияние орографии,
- сооружения повышенного уровня ответственности.
Заключение. В статье приведен алгоритм определения ветровой нагрузки с помощью СП 20.13330.2016. Даны определения и физический смысл терминам «основная ветровая нагрузка», «пиковая ветровая нагрузка», а также аэродинамическим коэффициентам которые используются в руководящем документе. Эти знания необходимы проектировщику для понимания терминов СП «Нагрузки и воздействия» и их правильного применения для расчета ветровых нагрузок.